
As I have shown in my articles on eclipse theory, the Moon does not have to be exactly on the Sun-Earth line in order for there to be an eclipse. In the case of a lunar eclipse, at the distance of the Moon's orbit the Earth's shadow is much wider than the Moon itself (about 23/4 times as wide, in fact) so the Moon does not even have to be in the centre of it for there to be a total eclipse, let alone a partial one. For solar eclipses the Moon's shadow is much narrower, but the Earth is sufficiently large that the shadow can still strike it somewhere even with the Moon considerably "off-axis".
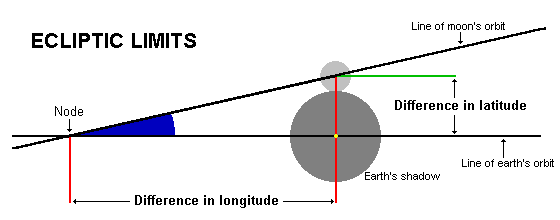
The maximum distance the Moon can be mis-aligned is called the Ecliptic Limit. This can be expressed as a difference in latitude (i.e. up/down distance) between the Moon and the Sun-Earth line at new or full Moon, or a difference in longitude (i.e. left/right distance) between the node and the line - see the diagram below, which is drawn looking straight along the Sun-Earth line, indicated by the yellow spot. The two measures are equivalent (as they are directly related by the angle between the plane of the Moon's orbit and the plane of the Earth's orbit, shown in blue) but can be useful in different circumstances. The latitudes of Sun and Moon are listed in tables of position called ephemerides (produced by such bodies as national observatories but also available online and from software programs) so eclipses can be predicted by consulting an ephemeris to see if the latitude difference is within the ecliptic limit at a given new or full Moon. On the other hand, knowing the distance from the node is more useful when dealing with orbital positions, as is the case when considering sequences of eclipses.

The calculation of ecliptic limits in latitude is "merely" a problem of geometry but, as with everything else to do with eclipses, it's not quite that simple! The easiest situation to visualise is a lunar eclipse. Clearly, the limiting case is when the disc of the Moon just touches the Earth's shadow, as shown in the diagram above. The ecliptic limit (the angle between the centre of the Moon and the Sun-Earth line - shown in blue) is thus half the angle spanned by the shadow at the distance of the Moon plus half the Moon's apparent (angular) diameter. It would be easy enough to calculate the width of the shadow (and hence its angle) in the case when the Moon is exactly on the Sun-Earth line but more difficult when it is above or below the line, as required for the limiting case - trigonometry doesn't really like curves! This approach will thus give an approximate value only (though a pretty close one). Fortunately, there is an accurate method of calculating the shadow angle at the correct point but it's a little less intuitive so I've done another diagram (which is, I think it goes without saying, not even remotely to scale!):-
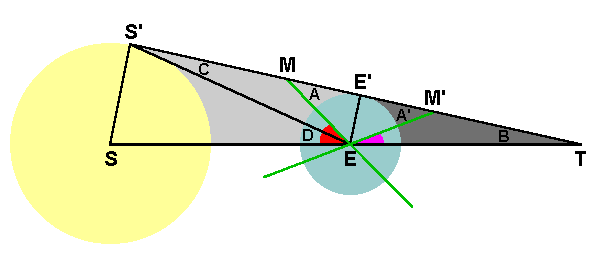
The diagram shows the Sun (in yellow), the Earth (in light blue), and the shadow of the Earth extending to the right. For clarity, the diagram shows the just upper part of the situation: the shadow cone does of course extend below the Sun-Earth line as well as above. Point S is at the centre of the Sun, S' is at its edge. Similarly, point E is at the centre of the Earth and E' is at its edge. T marks the very tip of the Earth's shadow (shown in dark grey). Line SET is thus the Sun-Earth line mentioned above, now seen as an actual line because the viewpoint of this diagram is at 90degrees to the first one (i.e. from its left or right side).
It should be apparent that an eclipse of some sort must occur whenever the Moon encroaches below the line running from S' to T. The eclipse will be solar if the Moon is to the left of E' (encroaching into the region of visibility of the solar disc as seen from the Earth, shown in light grey) and lunar if it is to the right (encroaching into the Earth's shadow). Point M is the limiting case for a solar eclipse, point M' for a lunar eclipse, given that the lines EM and EM' are both radii of (different) lunar orbits, shown edge-on in green. Relevant angles are labelled A to D (note that the two angles marked A and A' are, in fact, the same size because, as we just have an eclipse in both cases, each of the orbits must be at the same [maximum] angle to Earth's equator - not shown [for clarity], but lying parallel to S'E'T).
The required shadow angle for lunar eclipses, which I shall call X, is shown in purple. Geometry tells us that angle A' = X + B [ as the unlabelled angle at M' is equal to both 180-(X+B) and 180-A' ] and that angle D = B + C [ by a similar argument ]. Re-arranging these two equations to eliminate B gives us the result X = A' + C - D. Repeating the analysis for the angle in red (which I shall call Y), the required angle for solar eclipses, gives the answer Y = A - C + D. The details of the proof are left as a rather easy "exercise for the student"! Not much progress you might think, but angles A (or A'), C and D are in fact well-defined, easily calculated values - A is the parallax of the Moon, C the parallax of the Sun and D the angular semi-diameter of the Sun. Er - what?? Well, an object's parallax is the amount it shifts against a distant background when viewed from different positions. To see this effect in action, hold up a finger at arm's length and view it firstly with your left eye and then with the right - see the movement? For the Moon and Sun, parallax is defined as the shift against the stars when the viewpoint moves from the centre of the Earth to a pole. Given that viewing from the centre of the Earth does present practical problems (!), the value is usually calculated from the Earth's radius and the distance of the Sun or Moon. More obviously, the semi-diameter is just half the apparent size of the object in the sky when viewed from the centre of the Earth - also usually calculated rather than measured. It is more helpful to use sensible letters in the results, rather than the arbitrary ones on the diagram, so if we say that P(x) is the parallax of object x and D(x) is its semi-diameter, then X = P(moon) + P(sun) - D(sun) and Y = P(moon) - P(sun) + D(sun).
| So, we are now in a position to achieve our initial aim - to derive an expression for the lunar ecliptic limit. We know the shadow angle (X), and half the Moon's apparent diameter is simply D(moon) in the above terminology. Abbreviating to initial letters, the answer is thus "P(m) + P(s) - D(s) + D(m)" - phew!! This is of course the limit for a partial eclipse: the limit for a total eclipse is found in a similar way but now the Moon has to be just fully within the shadow and so the limit is the shadow angle minus half the diameter, that is P(m) + P(s) - D(s) - D(m). [see diagram on right] | 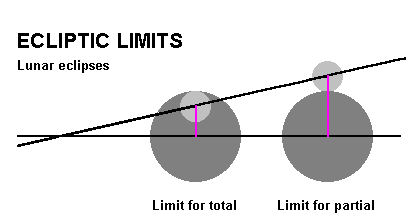 |
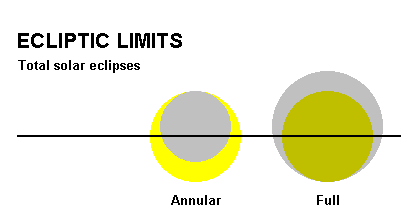 It would be tempting to think that the same sort of calculations we've done for lunar eclipses would hold good for solar eclipses and, just for once, it's true! [well, nearly]. Although we're dealing with encroachment onto the solar disc in this case the basic geometry is the same, so using the result for angle Y derived above we may say that the ecliptic limit for partial solar eclipses is P(m) - P(s) + D(s) + D(m) and for totals P(m) - P(s) + D(s) - D(m). The "nearly" has to do with the assumption made in the above analyses that the totality of an eclipse is established by the top edge of the Moon. The top edge criterion is always true for total lunar eclipses as the apparent size of the Moon is always smaller than that of the Earth's shadow. This is why all total lunar eclipses are full i.e they all darken the entire disc of the Moon rather than sometimes leaving a bright border around the shadow. Total solar eclipses are different, however, in that because of its somewhat eccentic orbit and therefore varying distance from the Earth the apparent size of the Moon is sometimes larger than that of the Sun (giving a full eclipse) and sometimes smaller (giving an annular eclipse). Annular eclipses satisfy the "top edge" criterion but full eclipses do not: a full eclipse is established by the bottom edge of the Moon just reaching the far side of the Sun's disc, not by the top edge just entering it [see diagram - Sun shown in yellow, Moon's shadow in grey]. The consequence is that in the case of a total solar eclipse the ecliptic limit is greater for full eclipses than for annulars. It's quite easy to allow for this mathematically, fortunately - one simply has to replace the term involving semi-diameters, "+ D(s) - D(m)", by "- D(s) + D(m)" to give the situation for a full eclipse, or just write "+ ABS{D(s) - D(m)}" to cover both cases at the same time. [The ABS operator gives the absolute value of a number i.e. converts a negative value to positive but leaves a positive one alone]. However, while it might be simple to allow for this phenomenon, as with many aspects of ecliptic limits I haven't actually found this issue mentioned in any other analysis. I presume I can't be the first person to have thought of it but I may be one of the first to have put it in print!
It would be tempting to think that the same sort of calculations we've done for lunar eclipses would hold good for solar eclipses and, just for once, it's true! [well, nearly]. Although we're dealing with encroachment onto the solar disc in this case the basic geometry is the same, so using the result for angle Y derived above we may say that the ecliptic limit for partial solar eclipses is P(m) - P(s) + D(s) + D(m) and for totals P(m) - P(s) + D(s) - D(m). The "nearly" has to do with the assumption made in the above analyses that the totality of an eclipse is established by the top edge of the Moon. The top edge criterion is always true for total lunar eclipses as the apparent size of the Moon is always smaller than that of the Earth's shadow. This is why all total lunar eclipses are full i.e they all darken the entire disc of the Moon rather than sometimes leaving a bright border around the shadow. Total solar eclipses are different, however, in that because of its somewhat eccentic orbit and therefore varying distance from the Earth the apparent size of the Moon is sometimes larger than that of the Sun (giving a full eclipse) and sometimes smaller (giving an annular eclipse). Annular eclipses satisfy the "top edge" criterion but full eclipses do not: a full eclipse is established by the bottom edge of the Moon just reaching the far side of the Sun's disc, not by the top edge just entering it [see diagram - Sun shown in yellow, Moon's shadow in grey]. The consequence is that in the case of a total solar eclipse the ecliptic limit is greater for full eclipses than for annulars. It's quite easy to allow for this mathematically, fortunately - one simply has to replace the term involving semi-diameters, "+ D(s) - D(m)", by "- D(s) + D(m)" to give the situation for a full eclipse, or just write "+ ABS{D(s) - D(m)}" to cover both cases at the same time. [The ABS operator gives the absolute value of a number i.e. converts a negative value to positive but leaves a positive one alone]. However, while it might be simple to allow for this phenomenon, as with many aspects of ecliptic limits I haven't actually found this issue mentioned in any other analysis. I presume I can't be the first person to have thought of it but I may be one of the first to have put it in print!
In the case of lunar eclipses, if an event happens at all it will be visible over an entire hemisphere of the Earth because both the Moon and the observers are within the Earth's shadow. This is not the case for solar eclipses, as the Moon's shadow forms a narrow cone which only covers a small area when it strikes the Earth. The solar ecliptic limits given above define the case where just the "side" of the cone nearest to the Earth barely grazes its surface: there is thus another (but less interesting) set of limits where the entire cone just strikes the Earth i.e. it is now the further side of the cone that makes grazing contact. The limits in these cases are P(m) - P(s) - D(s) - D(m) for a partial eclipse and P(m) - P(s) - ABS{D(s) - D(m)} for a total. My thanks to computational astronomer Paul Schlyter, of Stockholm, for this information, and also for confirming that my assertion about annular and full eclipses above is correct.
Lunar eclipses have their complicating factor too, however, in that the Earth's atmosphere slightly bends the Sun's light as it passes through - the phenomenon of refraction. This means that the shadow cast by the Earth is actually slightly larger than "straight-line geometry" would predict and so a compensating factor has to be added. There is no such compensation required for solar eclipses, of course, as the Moon does not have an atmosphere. The extent of the shadow enlargement can be determined by observation and measurement but, as the shadow is slightly "fuzzy" as a result of the refraction, the process involves a degree of judgement. The factor is not a definite number, therefore, and so varies depending on the learned body involved!
Compensation can be applied by one of two methods - by using a slightly greater "effective" shadow radius or by increasing the parallax of the Moon. Historically, the first method was used, with a value of 1/50. Following further research, however, the value 1/73 is more popular nowadays. The second method is more usually employed though, using a value of 1/85 - the so-called "French Rule". This is the method I have used in my calculations.
So, that's it then - time to generate some actual numbers? Oh dear me no! There's quite a long way to go yet!! The first issue concerns the fact that while the above diagrams and analyses are exactly correct for dealing with the limiting case when the Moon and Sun-Earth line have the same longitude (the situation called a "conjunction in longitude"), the angle thus found isn't actually the maximum angle by which the Moon can be mis-aligned and there still be an eclipse.
| To see this, look at the diagram to the right and consider what happens if we move the Moon down its orbit track (towards the node) - click or tap the diagram to make this happen. In the case of the partial eclipse the Moon starts to overlap the shadow a little and in the case of the total it begins to lie fully within the shadow i.e. we don't have a limiting case any longer. To get back to limiting cases we need to find the point of maximum overlap/immersion (which will in fact be when the purple lines are at right angles to the Moon's orbit track) and then move the Moon "up and left" a bit so edges are just touching once more - click/tap again to achieve this. In this position the angle between the Sun-Earth line and the centre of the Moon will be the same as it was at the conjunction in longitude position (half the shadow angle plus or minus half the Moon's diameter), so we can still use the above formulae for this. However, we now need to calculate what the angle will be when the conjunction in longitude is restored i.e. at the instant of true full Moon, as this is the instant used in the definition of the ecliptic limit - click/tap one final time to show this. | 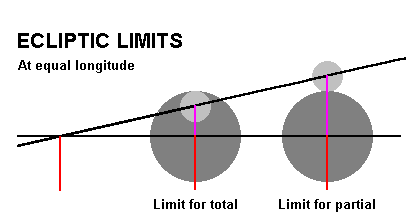 |
When we moved the Moon down its orbital line, it was not because we were taking into account the passage of time but just to establish a particular starting position. Having done that, we cannot now arbitrarily move it back up (to achieve conjunction in longitude) because we need to simulate a physical process - the movement of the Sun, Earth and Moon in the time between conjunction and the eclipse - not just re-adjust the geometry. An apparently simple problem thus becomes a rather complicated one - to calculate the length of the purple line at the instant it is at right-angles to the line of Earth's orbit, given that both the Moon and the Earth are moving! Click/tap one more time to see this position.
I will freely admit that I had to look this one up so I shall just present the answer rather than give the proof (sighs of relief!). It turns out that we need to multiply the length of the purple line at the "true maximum limit" position by a numerical factor to give its length at conjunction. The value of this factor is determined by the angle between the orbit of the Moon and that of the Earth, and the degree to which the Moon is moving in longitude faster than the Earth (relative to the node). As I have said on a number of occasions in my dissertations on eclipses, the angle is just about the same for all eclipses (very close to its maximum value) and the calculation isn't particularly sensitive to the second parameter (which varies by about +/-18% from its mean value), so the factor itself is virtually constant, with a value of 1.005 i.e. the difference in latitude at conjunction must be increased by 0.5% in order to take the "line of closest approach" effect into account - not a lot, to be sure, but enough to make a difference when calculating the ecliptic limit in longitude.
| To see the whole thing in action, click or tap on this final diagram. It is clear that the difference in longitude (the distance between the red lines) increases firstly as a result of using the true maximum limit and then because of measuring at full Moon/conjunction. Note that, although in the final diagram the Earth's shadow is not actually fully across the Moon (for the case of a total eclipse) or touching it (for the case of a partial eclipse) these positions will produce "grazing" instances of total or partial eclipses either just before or just after the diagrammed position, when both bodies will be in a slightly different place on their orbits, and so these positions are truly the ecliptic limits. It should however be noted that the actual eclipse does not happen at the exact instant of full Moon but rather just before (if the Monn is ascending on its orbit) or just after (if it is descending), as can be seen in actual data. |  |
Right then, time for a deep breath as we're nearly there now! Given that we have a right-angled triangle it might seem we could calculate the limit in longitude with a bit of simple trigonometry involving the limit in latitude (the purple line in the diagrams above) and the angle at the node. By now though, you'll realise that would be just too easy! The problem is that the lines on the diagrams are not really straight: being orbits or lines of latitude and longitude they are actually curved in the dimension into/out of the page. This hasn't mattered so far as we have always been using angles, not distances, and doing calculations along the same line: the line of latitude which crosses the Sun-Earth line (another reason why it was important to use the instant of conjunction as our defining point). To calculate the limit in longitude we must (by definition) move away from this line and so it is necessary to use theorems from spherical geometry. Fortunately, a certain Mr Napier had it all worked out quite some time ago and the theorem we want is Napier's Second Rule: not very complicated but I'm still going to leave it as homework! (try "napier rule" in Google).
The final nuance concerns the angle at the node (i.e. the inclination of the Moon's orbit). I've always been careful to say this angle is nearly the same for all eclipses because there is a slight variation depending on how far the node is away from the Sun-Earth line: about 0.4%, in fact (again small, but these little differences do add up!). This is because the inclination is affected by the exact positions of Moon, Earth and Sun, due to the complex interactions between them mentioned in my other articles. Using the same techniques as I used to prove that the angle was near-maximum at eclipse, it is possible to allow for these interactions and thus derive an inclination for a given longitude difference.
Must be time for a fanfare of trumpets now, as we're finally ready to plug in actual values and derive some answers!! This does introduce another uncertainty though, as of course the results you get out of any formula depend on the numbers you put in. The accepted values for things like the Moon's diameter have changed over the years as measurement accuracy has increased, and lunar orbit theory has improved very considerably only quite recently. This means that comparing one's own results with tabulated values is difficult as it's often impossible to know what input data were used by other people. Bearing this in mind, I set up a spreadsheet in such a way that I could use various versions of the "accepted" figures and thus see under what circumstances my answers agreed with those in standard reference works (assuming they agreed at all!).
In order to see what data we need, I shall remind you that the expressions I derived involve the parallax and semi-diameters of the Sun and Moon (in various combinations) and that the correction factor and conversion to a difference in longitude both need the inclination of the Moon's orbit. Parallax can be calculated knowing the diameter of the Earth and the distance of the body, and angular semi-diameter likewise from the actual diameter of the body and its distance. We thus only need to know the diameter of Sun, Earth and Moon and the maximum and minimum distance of the Earth from the Sun and of the Moon from the Earth. The maxima and minima are needed because to maximise the values of the expressions, i.e. to derive the actual ecliptic limits, if we are adding a value we need it to be large but if subtracting then it must be small. However, we must beware of (possibly) the final pitfall in all of this: for an absolute maximum we may need one value to be large and, at the same time, another to be small - but this might not be physically possible! For instance, a body cannot simultaneously have a large parallax and a small semi-diameter - the former would imply it is near to us but the latter means it's far away. Choices thus have to be made as to which valid combinations of values will give the optimum result. It seemed to me as I began to write this article that this nuance had been overlooked by the Institute of Celestial Mechanics at the Observatory of Paris (no less) in their website section covering some of the ground I have explored here. Having done my own calculations it became clear that they had indeed made this mistake so, with some trepidation, I emailed them - fortunately, they agreed with me completely! A little victory for the amateurs, I think.
So, how have I chosen my input values? The diameters of Earth and Sun came from the NASA/JPL Horizons website (and closely agree with other sources). The Earth-Sun distances were calculated using the current eccentricity of the Earth's orbit and the official definition of the average distance, called an Astronomical Unit. The diameter of the Moon was calculated using the ratio between it and the Sun's diameter adopted by the Astronomical Ephemeris to represent the effective radius for eclipses (i.e. allowing for its uneven limb profile). The extreme Moon-Earth distances were taken from Jean Meeus' book 'Mathematical Astronomy Morsels', chapter 2. Calculation of the (effective) inclination of the lunar orbit for a given Sun-Earth-Moon orientation proved to be particularly difficult as I could find no documented method for doing this. Emails were thus sent out to other mathematical astronomers mentioned on the Internet and a further reply from Paul Schlyter, already mentioned above, gave me a (rather complicated!) way of calculating inclination from the output of a spreadsheet by Keith Burnett I already used to calculate lunar latitude, longitude and distance. This is itself ultimately derived from the latest lunar theory of Chapront via Meeus' book 'Astronomical Algorithms'. I am thus as confident as I can be that my data and methods are those currently accepted as correct.
The section you were beginning to think we'd never get to! The tables below show the actual input values I used and the answers they generated:-
|
|
| Limit in Latitude | Limit in Longitude | |||||
|---|---|---|---|---|---|---|
| Major limit | Minor limit | Major limit | Average | Minor limit | ||
| Partial solar | 1deg 35min | 1deg 25min | 17deg 24min | 16.42deg | 15deg 27min | |
| Partial lunar | 1deg 4min | 0deg 53min | 11deg 32min | 10.58deg | 9deg 37min | |
| Total solar (full) Total solar (annular) | 1deg 2min | 0deg 55min | 11deg 22min 11deg 15min | 10.64deg | 9deg 58min | |
| Total lunar | 29min 54sec | 23min 41sec | 5deg 23min | 4.82deg | 4deg 16min | |
And how close are they to values quoted elsewhere? Well - one must firstly disregard many values listed in text books (and references found via Google and the like!) as they have clearly been generated under false assumptions. The favourite error is to use the minimum possible inclination for the Moon's orbit when calculating major limits. This gives much larger values but all such results are totally wrong: I have stated several times above that the inclination is in fact near to the maximum at an eclipse. Then I think we must ignore the oft-quoted values of 6deg 0min and 3deg 45min for the major and minor longitude limits for a total lunar eclipse: these are clearly well off-beam but I've no idea how they were generated. This leaves us with a much smaller set of values which one might believe in. Unfortunately, many of these are in very old books so use data that is no longer quite correct. They also feature analyses that are not complete, often omitting the corrections for "true maximum limit" and the movement of both Sun and Moon needed to achieve conjunction in longitude, and sometimes do not use spherical geometry. The values quoted are thus usually smaller than mine by several arc-minutes. There is then a considerable paucity of quoted values for total eclipses of both sorts, making comparison difficult.
Jean Meeus comes to our aid again to a large extent though, as 'Mathematical Astronomy Morsels III' quotes values for many of the limits in longitude (on pages 112, 113 & 124), derived from the work of Danjon [ironically, a past Director of the Paris Observatory mentioned above!]. Taking these values into account, my results differ by at most 3arc-minutes from the "most popular" believable values. This level of difference can probably be explained by other sources taking slightly different values for the input parameters and, in particular (due to the problems mentioned above), for the inclination of the lunar orbit. I didn't find many lists of limits in latitude, the most comprehensive being those quoted by the Institute of Celestial Mechanics which, as I've already said, turned out to be not quite accurate! When corrected, the results differ by only a few seconds of arc, due simply to very slightly different input parameters: not surprising, as we use identical methods. I am thus entirely happy that my results can be taken as the "true" answers.
However! They are only true under the initial assumptions made. The problem is that recent work by Meeus has shown that the extreme maximum and minimum distances of the Moon from the Earth cannot happen at an eclipse! (see 'Mathematical Astronomy Morsels III', page 17). It is thus clear that the above limit values are not correct in the "real-world" situation (in the same sense that answers using the minimum inclination value are not correct). The same spreadsheet as mentioned above in connection with the calculation of inclination allows the true distances to be calculated, however. As with the inclination, the distances depend on whether the Earth is at aphelion or perihelion, whether it is new Moon or full Moon, whether the Moon is at apogee or perigee, and how far the Moon is away from the node. Taking these factors into account makes a difference of about 1minute of arc, decreasing the major limits and increasing the minor ones. The effect is greater for lunar eclipses than for solar, as their limits are determined by the Moon's perigee distance at aphelion, which is most affected by the orientation of the Moon's orbit.
Given the small corrections involved I shall not repeat all the above tables, just the one for limits in longitude as these are the values most-often quoted:
| Limit in Longitude | |||
|---|---|---|---|
| Major limit | Average | Minor limit | |
| Partial solar | 17deg 23min | 16.42deg | 15deg 28min |
| Partial lunar | 11deg 30min | 10.57deg | 9deg 38min |
| Total solar (full) Total solar (annular) | 11deg 19min 11deg 14min | 10.62deg | 9deg 58min |
| Total lunar | 5deg 23min | 4.84deg | 4deg 17min |