Precession and Nutation - a mathematical treatment
Preamble
On the main page dealing with the stability of the Earth's rotational axis I described how a force due to the gravitational attraction of the Sun and Moon acting on the asymmetry of the Earth would, instead of changing the tilt of the axis, cause the direction of point of the axis to describe a circle at constant inclination. While the description given there was basically accurate, it gave no insight into the processes involved. This was a deliberate decision, as a rigorous explanation of precession usually involves some rather difficult mathematics. However, I felt I should be able to come up with an accurate description which explains as much of the mathematical formalism as possible. A lot of research and head-scratching later, here's my attempt! [which is, I freely admit, almost entirely based on a series of lectures authored by Richard Fitzpatrick at the University of Texas, but with considerable additional explanatory material added by myself]. A further "health-warning" though - despite being (to me) a more understandable treament than that given by the standard texts, what follows is not going to be understood by anyone who does not have a fair grasp of trigonometrical mathematics and algebra. You have been warned!
Introduction
The main difficulty that any description of precession must address is that the motions of the bodies involved (Sun, Moon and Earth) are all in different planes, which means that the forces involved are also. Furthermore, the relationship of those planes to each other is constantly changing, which adds considerable further complication. Any attempt to analyse the situation in terms of conventional spatial geometry is thus certain to involve very complex expressions involving strings of sine and cosine operators to deal with the relationships between the angles involved. The original analysis by Leonhard Euler (based on earlier work by d'Alembert) took this approach, and is thus almost impenetrable (by me, anyway!). The breakthrough came when Joseph Louis Lagrange (1736-1813) devised a new system of mechanics. This is, fundamentally, just a different way of looking at Newtonian mechanics but with one crucial advantage - it is independent of the co-ordinate system in which it is expressed.
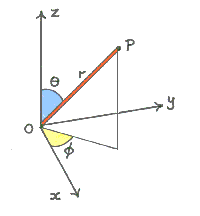 By "co-ordinate system" I mean the way in which the position of a point in space is specified. The two most common systems are Cartesian, where the position is given relative to a 3-dimensional grid, and Polar, where the position is given in terms of angles and the distance from the origin of the co-ordinates. The diagram shows the same point, P, described by both systems: the Cartesian co-ordinates are x, y, z and the Polar co-ordinates are phi [yellow angle], theta [blue angle], r [radial distance]. However, while this is fine for describing points, when one is working with planes an expression giving (for example) the distance between a point on one plane and a point on another plane involves conversions between the co-ordinate systems describing each plane, which is where all the sines and cosines come in. Lagrange discovered a formalism which, once the initial work to derive its components had been done, did not involve any further conversion gymnastics. He found that if one could derive expressions for the kinetic energy, K, and potential energy, U, of a system, the overall expression representing K - U (called the "Lagrangian" of the system, in his honour) could be manipulated according to simple rules to derive results corresponding to Newtonian mechanics (such things as Force = Mass x Acceleration and Conservation of Momentum). These rules were themselves derived by using the Principle of Least Action, which says that a system proceeds from one state to another via "the line of least resistance" (but expressed mathematically!). The optimal path will usually be a function both of the route taken and the speed at which various parts of the route are traversed. There is a clear analogy here with the different options offered by satnav devices: you can get from A to B either by going slowly on a short country road or faster on a longer motorway. This tradeoff between distance (i.e. change of co-ordinates) and speed (i.e. rate of change of co-ordinates) reflects directly into the precession case - an attempt to change an angular co-ordinate (by the gravitational attraction tending to alter the obliquity) actually results in a change in rotational speed (the motion of precession). The Lagrangian has given us our first insight!
By "co-ordinate system" I mean the way in which the position of a point in space is specified. The two most common systems are Cartesian, where the position is given relative to a 3-dimensional grid, and Polar, where the position is given in terms of angles and the distance from the origin of the co-ordinates. The diagram shows the same point, P, described by both systems: the Cartesian co-ordinates are x, y, z and the Polar co-ordinates are phi [yellow angle], theta [blue angle], r [radial distance]. However, while this is fine for describing points, when one is working with planes an expression giving (for example) the distance between a point on one plane and a point on another plane involves conversions between the co-ordinate systems describing each plane, which is where all the sines and cosines come in. Lagrange discovered a formalism which, once the initial work to derive its components had been done, did not involve any further conversion gymnastics. He found that if one could derive expressions for the kinetic energy, K, and potential energy, U, of a system, the overall expression representing K - U (called the "Lagrangian" of the system, in his honour) could be manipulated according to simple rules to derive results corresponding to Newtonian mechanics (such things as Force = Mass x Acceleration and Conservation of Momentum). These rules were themselves derived by using the Principle of Least Action, which says that a system proceeds from one state to another via "the line of least resistance" (but expressed mathematically!). The optimal path will usually be a function both of the route taken and the speed at which various parts of the route are traversed. There is a clear analogy here with the different options offered by satnav devices: you can get from A to B either by going slowly on a short country road or faster on a longer motorway. This tradeoff between distance (i.e. change of co-ordinates) and speed (i.e. rate of change of co-ordinates) reflects directly into the precession case - an attempt to change an angular co-ordinate (by the gravitational attraction tending to alter the obliquity) actually results in a change in rotational speed (the motion of precession). The Lagrangian has given us our first insight!
Calculation of the Lagrangian for the Earth-Sun system
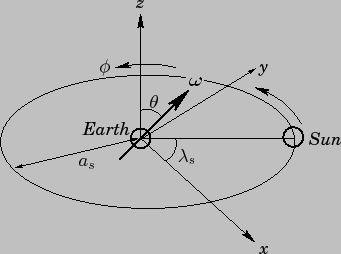
Right then - let's derive a Lagrangian! I shall start with the Earth-Sun system, as that is the easiest case, in a co-ordinate system centred on the Earth i.e. I shall be working as if the Sun orbited the Earth, not the other way round. This is perfectly permissible from a mechanics point of view (as long as we remember that it is really the Earth that is moving) and makes things easier when we come to consider the system involving the Earth and both the Sun and the Moon. As shown by the next diagram, I shall call the obliquity of the Earth's spin axis , and the angle it makes with the x-y axis
, and the angle it makes with the x-y axis 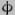 . I shall further assume that the line from the centre of the Earth to the centre of the Sun makes an angle
. I shall further assume that the line from the centre of the Earth to the centre of the Sun makes an angle 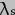 with the x-axis.
with the x-axis.
Kinetic Energy
We firstly need to find expressions for the kinetic and potential energies of the system. The kinetic energy is perhaps the most straightforward, as it is simply the sum of the [rotational] energy of the Earth along its x, y & z axes. The x-axis can be though of as running through the Earth at the equator from 0deg to 180deg longitude, with the y-axis as equatorial from -90deg to +90deg longitude and the z-axis running from pole to pole. Rotational kinetic energy is defined as 1/2 times the Moment of Inertia multiplied by the square of the rotational speed, where the Moment of Inertia is a quantity which takes into account the amount of mass rotating and the distance of the elements of that mass from the axis of rotation. Because the Earth has an equatorial bulge, the Moment of Inertia along the polar axis will differ from that along the equatorial axes. However, because the bulge is the same shape all the way round the equator, the Moment of Inertia along each equatorial axis will be the same. I shall call the polar Moment 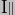 and the equatorial Moment
and the equatorial Moment 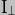 . I shall call the Earth's rotation on its [polar] axis
. I shall call the Earth's rotation on its [polar] axis  .
.
The rotational kinetic energy along the polar axis is therefore 1/2 times 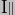 times
times  2, with similar expressions for the two equatorial axes. These values are relative to the Earth's own local frame of reference however, which is tilted with respect to the frame of reference of the Solar System as a whole which we are using for our calculations. Before using the expressions for kinetic energy in the Lagrangian we must therefore transform our local co-ordinates into global co-ordinates. This is the sort of transformation of frames of reference that use of the Lagrangian will avoid, but it has to be done initially in order to set up the Lagrangian in the first place. Fortunately, the way to do this was worked out by Euler (yes - him again!) so I shall just quote the result rather than work you through it.
2, with similar expressions for the two equatorial axes. These values are relative to the Earth's own local frame of reference however, which is tilted with respect to the frame of reference of the Solar System as a whole which we are using for our calculations. Before using the expressions for kinetic energy in the Lagrangian we must therefore transform our local co-ordinates into global co-ordinates. This is the sort of transformation of frames of reference that use of the Lagrangian will avoid, but it has to be done initially in order to set up the Lagrangian in the first place. Fortunately, the way to do this was worked out by Euler (yes - him again!) so I shall just quote the result rather than work you through it.
Euler found that it requires at most three "twists" of a given frame of reference to align it with any other frame of reference. The first two must be taken in the 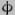 and
and  directions, and the third is in the
directions, and the third is in the 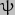 direction. This is not shown on the diagram above but in this case it is effectively a twist around the Earth's axis of rotation. The
direction. This is not shown on the diagram above but in this case it is effectively a twist around the Earth's axis of rotation. The 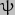 twist is not actually needed though, as the plane of the Earth's equator is inclined to the general plane of the solar system in one axis only. Euler's work shows us that, with
twist is not actually needed though, as the plane of the Earth's equator is inclined to the general plane of the solar system in one axis only. Euler's work shows us that, with 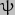 = 0, the components of angular velocity round the x, y & z axes are transformed thus:-
= 0, the components of angular velocity round the x, y & z axes are transformed thus:-
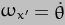


The 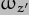 component is, of course, just the Earth's axial rotation,
component is, of course, just the Earth's axial rotation,  , a fact we shall use later.
, a fact we shall use later.
Note that these expressions use the mathematical shorthand that a velocity in a given direction is shown by putting a dot over it. [The dot actually means "the differential with respect to time" - velocity is, however, the differential of a distance or angle with respect to time]. Note also that 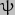 = 0 simply means that there is no rotational offset in the
= 0 simply means that there is no rotational offset in the 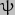 direction between the local and global co-ordinate systems - it does not mean that the angular velocity in this direction,
direction between the local and global co-ordinate systems - it does not mean that the angular velocity in this direction,  , has to be zero as well.
, has to be zero as well.
So, bearing in mind we have to use the square of each component of angular velocity, the expression we get for the total rotational kinetic energy is:-

Potential Energy
That's only half the job done though, as we now need an expression for the total potential energy. In the case of an orbiting body, the "potential" is the gravitational potential. For the Earth-Sun system, this is the sum of the gravitational potential generated by the body of the Earth as a whole and the potential generated by the asymmetries of the Earth such as the equatorial bulge. Anyone who has read my treatise on The Tides will know that the first potential has a simple 1/r dependence whereas the second has a more complex inverse-cube form. In fact, the total gravitational potential generated by an asymmetric body at distance r and angle 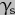 is:-
is:-

where G is the universal gravitational constant and M is the mass of the body. P2 is a function that describes the shape of the equatorial bulge, known as the Legendre polynomial of order 2. Fortunately, its form is quite simple:- P2(A) = 1/2(3cos2A - 1). Again, those who have read my treatise on The Tides will recognise this as also describing the tidal equipotential surface.
In the case of the Earth-Sun system the difficult part of this expression is 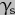 , as it must be calculated in 3-dimensions i.e. it is not just 90 -
, as it must be calculated in 3-dimensions i.e. it is not just 90 - . In fact, a bit of swift trigonometry will soon show that cos
. In fact, a bit of swift trigonometry will soon show that cos 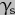 = sin
= sin sin
sin 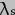 . So, given that the potential energy of the system is the gravitational potential of the Earth multiplied by the mass of the Sun, if we plug in all the above expressions we get:-
. So, given that the potential energy of the system is the gravitational potential of the Earth multiplied by the mass of the Sun, if we plug in all the above expressions we get:-
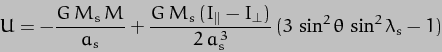
This result can be simplified somewhat, however, in order to make the next step of the argument clearer. The first simplification is actually an approximation, to which I shall return later. It involves the recognition that the precession period is actually very much greater than a year and so the sin2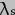 factor due to the apparent motion of the Sun can be averaged over a year, to give the value 1/2. This enables us to apply a standard trigonometric identity to convert the sin2
factor due to the apparent motion of the Sun can be averaged over a year, to give the value 1/2. This enables us to apply a standard trigonometric identity to convert the sin2 term to -cos 2
term to -cos 2 . Next, Kepler's Third Law tells us that the square of the orbital period is related to the cube of the orbital distance, and then we can define a number of auxiliary variables just to tidy things up. Finally, because the Principle of Least Action deals with changes to things, not constant values, all the constant factors can be taken out of the expression and lumped together so they can drop out of the analysis later. The result of all this is a much cleaner expression for U:-
. Next, Kepler's Third Law tells us that the square of the orbital period is related to the cube of the orbital distance, and then we can define a number of auxiliary variables just to tidy things up. Finally, because the Principle of Least Action deals with changes to things, not constant values, all the constant factors can be taken out of the expression and lumped together so they can drop out of the analysis later. The result of all this is a much cleaner expression for U:-
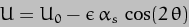
where  is the "grand constant", and the auxiliary variables are
is the "grand constant", and the auxiliary variables are


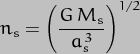 (by Kepler's Third Law)
(by Kepler's Third Law)
The Lagrangian
We are now ready to put everything together to give the Lagrangian, and then to apply the Principle of Least Action! The Lagrangian is, of course, K - U, which from the above results is
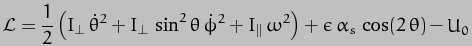
It is important to realise at this point that energy is a scalar and not a vector i.e. it has a magnitude but not a direction. Given that each term in the Lagrangian is a component of the total energy of the system, this means the expression as a whole is a scalar and so can be manipulated without having to worry about frames of reference and the transformations required to move between them. This is the massive advantage of the Lagrangian formulation.
The Principle of Least Action
It's now time to examine this Principle a little more closely, so we can use it on the Lagrangian we have derived. Unfortunately, as it is defined in strictly mathematical terms it is difficult to accurately express its meaning in words - I'll have a go though. What it says is that the variation with time of the change in the Lagrangian due to a velocity along one of the co-ordinates is equal to the change in the Lagrangian due to a displacement along that co-ordinate. All clear? No, I thought not. Maybe better to hold on to the approximate meaning of the speed/distance tradeoff. In mathematical terms, with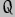 as an arbitrary co-ordinate of the system, the Principle is defined as:-
as an arbitrary co-ordinate of the system, the Principle is defined as:-

where all the "d's" indicate the operation of differentiation, which is the mathematical way of calculating the change in one thing due to a change in the other.
If we take as our co-ordinate, the only part of the Lagrangian which has
as our co-ordinate, the only part of the Lagrangian which has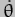 in it is the first component of the kinetic energy part. The change in the Lagrangian resulting from a change in
in it is the first component of the kinetic energy part. The change in the Lagrangian resulting from a change in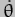 is thus the differential of this component only. However, if we assume precession at constant obliquity,
is thus the differential of this component only. However, if we assume precession at constant obliquity,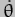 is zero and so the differential will also be zero. The Least Action formula thus reduces to
is zero and so the differential will also be zero. The Least Action formula thus reduces to
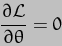
To calculate the value of this expression we will further assume that both  and
and  are constant, i.e. steady precession and constant spin rotation. We already know that
are constant, i.e. steady precession and constant spin rotation. We already know that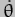 is zero, and of course the differential of the constant
is zero, and of course the differential of the constant 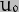 will be zero, so only the middle three elements of the Lagrangian need be considered.
will be zero, so only the middle three elements of the Lagrangian need be considered.
Standard texts on the differentiation of trigonometric functions tell us that the differential of sin2 is 2sin
is 2sin cos
cos , which is equal to sin 2
, which is equal to sin 2 . Given that, as stated above,
. Given that, as stated above,  = cos
= cos
 +
+  , the differential of
, the differential of  2 is -2
2 is -2 sin
sin
 . The differential of cos 2
. The differential of cos 2 is -2sin 2
is -2sin 2 . Differentiating the entire Lagrangian with respect to
. Differentiating the entire Lagrangian with respect to thus gives us
thus gives us

The final goal is now in sight! There is one last simplification to be made, however. We know that the precession rate,  , is very small (as the precession period is of the order of tens of thousands of years) whereas the Earth's spin rate,
, is very small (as the precession period is of the order of tens of thousands of years) whereas the Earth's spin rate,  , is quite large (a period of just 24hrs). Therefore,
, is quite large (a period of just 24hrs). Therefore,  2 must be much smaller than
2 must be much smaller than 
 and so the first term in the expression can be ignored in comparison with the other two. A bit of algebraic manipulation to get
and so the first term in the expression can be ignored in comparison with the other two. A bit of algebraic manipulation to get  on its own (together with use of the relationship sin 2
on its own (together with use of the relationship sin 2 = 2sin
= 2sin cos
cos mentioned above) now reveals that the result we have been struggling so hard to find is
mentioned above) now reveals that the result we have been struggling so hard to find is

Substituting the value of  back into this expression gives us the final answer - the precession rate of the Earth's spin axis due to the action of the Sun:-
back into this expression gives us the final answer - the precession rate of the Earth's spin axis due to the action of the Sun:-

This formula confirms that the precession is in the opposite direction from the Earth's spin (because of the minus sign) and is at 90deg to it (because we have derived an expression in  ). It also contains a lot of additional information: the precession rate is proportional to the asymmetry of the Earth's shape, as expressed by the "dynamic ellipticity factor"
). It also contains a lot of additional information: the precession rate is proportional to the asymmetry of the Earth's shape, as expressed by the "dynamic ellipticity factor"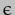 ; to the [apparent] orbit speed of the Sun,
; to the [apparent] orbit speed of the Sun, 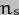 , squared; and to the cosine of the obliquity,
, squared; and to the cosine of the obliquity, . It is inversely proportional to the spin speed of the Earth,
. It is inversely proportional to the spin speed of the Earth,  .
.
To put it another way, the precession rate would increase if the Earth had a greater equatorial bulge; orbited the Sun more quickly (which is the same as saying "was nearer to the Sun"); had a smaller axial tilt; or had a slower spin rate.
In terms of actual numbers, if we plug in values for all the factors (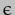 = 0.003358,
= 0.003358, 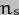 = 360 deg per year,
= 360 deg per year,  = 23.439deg,
= 23.439deg,  = 366.25636 x 360 deg per year), we find that the precession rate is 16.36 arc-seconds per year or one revolution in 79,218yrs [Note that 366.25636 is the number of sidereal days in a sidereal year]. This is somewhat greater than the currently accepted value, 15.95arc-sec/yr, because the value I used for
= 366.25636 x 360 deg per year), we find that the precession rate is 16.36 arc-seconds per year or one revolution in 79,218yrs [Note that 366.25636 is the number of sidereal days in a sidereal year]. This is somewhat greater than the currently accepted value, 15.95arc-sec/yr, because the value I used for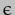 is calculated on the assumption that the Earth is homogeneous, which is not actually the case: the core is more dense than the mantle, and this reduces the moments of inertia. The true value of
is calculated on the assumption that the Earth is homogeneous, which is not actually the case: the core is more dense than the mantle, and this reduces the moments of inertia. The true value of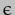 is difficult to calculate, as it requires a level of knowledge about the internal structure of the Earth we do not have - indeed, the observed value of the precession is used to improve this knowledge. The observed value is equivalent to one revolution in 81,260yrs.
is difficult to calculate, as it requires a level of knowledge about the internal structure of the Earth we do not have - indeed, the observed value of the precession is used to improve this knowledge. The observed value is equivalent to one revolution in 81,260yrs.
The influence of the Moon
The calculation of the additional effect the attraction of the Moon has on the spin precession rate of the Earth proceeds in a very similar fashion to that for the Sun alone, but with one very great difference. Not only is the orbit of the Moon inclined to the general plane of the solar system by an average of 5.16deg, but the plane of the orbit also precesses around the [global] z-axis (i.e. in the 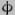 direction) at the rate of one revolution every 18.6yrs [actually 18.6133yrs relative to a co-ordinate system which takes the precession of the Earth's spin axis into account or 18.5998yrs relative to a fixed co-ordinate system]. This is an example of another type of precession, called orbital precession. In the same way that the Earth and its equatorial bulges can be regarded as a gyroscope, so can the entire Earth-Moon system. The non-spherical shape of the Earth is negligible at this scale and so the Earth acts as the shaft of the gyroscope with the Moon as the "wheel" - the "spin" factor is now its orbital rotation. The off-centre attraction of the Sun for the Moon on its tilted orbit now takes the place of the attraction of Sun and Moon for the Earth's bulges, resulting in a precession of the entire orbit of the Moon rather than of the body of the Earth - this is why this type of precession is called orbital precession. Spin precession and orbital precession are really the same thing, however - it's just the scale that has changed, not the basic principles.
direction) at the rate of one revolution every 18.6yrs [actually 18.6133yrs relative to a co-ordinate system which takes the precession of the Earth's spin axis into account or 18.5998yrs relative to a fixed co-ordinate system]. This is an example of another type of precession, called orbital precession. In the same way that the Earth and its equatorial bulges can be regarded as a gyroscope, so can the entire Earth-Moon system. The non-spherical shape of the Earth is negligible at this scale and so the Earth acts as the shaft of the gyroscope with the Moon as the "wheel" - the "spin" factor is now its orbital rotation. The off-centre attraction of the Sun for the Moon on its tilted orbit now takes the place of the attraction of Sun and Moon for the Earth's bulges, resulting in a precession of the entire orbit of the Moon rather than of the body of the Earth - this is why this type of precession is called orbital precession. Spin precession and orbital precession are really the same thing, however - it's just the scale that has changed, not the basic principles.
Potential Energy
It should, I hope, be apparent that the Kinetic Energy part of the Lagrangian will be unchanged by the addition of the Moon into the system, as it is the energy of the Earth alone we are considering. The non-coplanar nature of the Moon's orbit makes itself felt in the Potential Energy part and, in particular, in the calculation of the [3-D] angle between the Earth's spin axis and the Earth-Moon line, 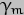 . In the Earth-Sun case, the components of the spin angular velocity have no dependence on
. In the Earth-Sun case, the components of the spin angular velocity have no dependence on 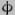 , which results in there being a zero x-component, and the Earth-Sun line is always in the global x-y plane and so has no z-component. The angle between the spin axis and the Earth-Sun line was thus composed only from the y-components of the two, resulting in the simple form cos
, which results in there being a zero x-component, and the Earth-Sun line is always in the global x-y plane and so has no z-component. The angle between the spin axis and the Earth-Sun line was thus composed only from the y-components of the two, resulting in the simple form cos 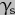 = sin
= sin sin
sin 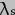 . The tilt of the Moon's orbit means the Earth-Moon line does have a z-component and, likewise, the dependence on
. The tilt of the Moon's orbit means the Earth-Moon line does have a z-component and, likewise, the dependence on 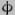 means the spin angular velocity has a non-zero x-component. This makes the expression for the angle between the spin axis and the Earth-Moon line rather more complex. As ever, I have moved the "tricky bits" to an extra page which interested parties can peruse by clicking here.
means the spin angular velocity has a non-zero x-component. This makes the expression for the angle between the spin axis and the Earth-Moon line rather more complex. As ever, I have moved the "tricky bits" to an extra page which interested parties can peruse by clicking here.
The answer is, however, that
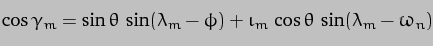
where 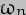 is the angle between the axis of the Moon's orbit and the co-ordinate x-axis and
is the angle between the axis of the Moon's orbit and the co-ordinate x-axis and 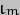 is the inclination of the Moon's orbit.
is the inclination of the Moon's orbit.
We must now insert this expression into the Legendre polynomial of order 2 involved in the expression for the potential energy of the system, which is (as given above), P2(A) = 1/2(3cos2A - 1). The cos2x part will result in a term in 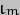 2 but as we know
2 but as we know 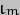 is small anyway this term will be considerably smaller and can thus be ignored. The term formed from the product of the two parts of cos
is small anyway this term will be considerably smaller and can thus be ignored. The term formed from the product of the two parts of cos 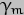 can be slightly simplified by use of the trigonometric identity sin 2A = sin A cos A and so the final result is:-
can be slightly simplified by use of the trigonometric identity sin 2A = sin A cos A and so the final result is:-
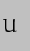
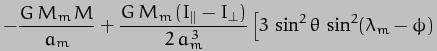
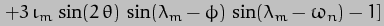
We can now make the same "averaging" approximation as we did in the Earth-Sun case, but over one lunar orbit this time rather than one solar orbit (i.e. year). Just as in the case of sin2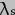 , the average of sin2(
, the average of sin2(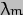 -
- 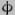 ) is 1/2. The average of sin(
) is 1/2. The average of sin(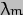 -
- 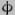 ) sin(
) sin(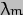 -
- 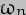 ) is more tricky to work out but if you expand the brackets by use of the identity sin (A-B) = sin A cos B - cos A sin B, on performing the multiplications you get one term in sin2
) is more tricky to work out but if you expand the brackets by use of the identity sin (A-B) = sin A cos B - cos A sin B, on performing the multiplications you get one term in sin2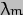 , one in cos2
, one in cos2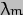 and two in sin
and two in sin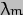 cos
cos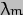 . The average value of the squared terms is again 1/2 but the average of the sin
. The average value of the squared terms is again 1/2 but the average of the sin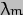 cos
cos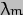 terms is zero. The end result is thus 1/2(cos
terms is zero. The end result is thus 1/2(cos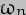 cos
cos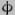 + sin
+ sin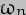 sin
sin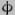 ) which, using the identity cos (A-B) = cos A cos B + sin A sin B, equals 1/2 cos(
) which, using the identity cos (A-B) = cos A cos B + sin A sin B, equals 1/2 cos(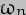 -
- 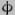 ).
).
So, if we again generate a number of auxiliary constants as follows:-

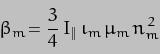
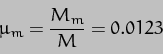
with 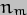 defined in an analogous way to
defined in an analogous way to  , we can again combine all the constant factors to produce
, we can again combine all the constant factors to produce
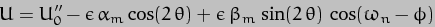
which has the same form as the corresponding expression for the Earth-Sun case, but with the addition of a further term due to the tilt of the Moon's orbit.
Sun plus Moon
Given that gravity is a "superposable force" i.e. is additive in its effect, we can add together the potential energy expressions for the Earth-Sun and Earth-Moon cases individually to produce an overall expression for the Earth-Sun-Moon system. This is:-
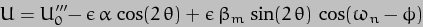
where  is the sum of
is the sum of  and
and 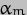 . We can now add this expression to that for the Kinetic Energy of the system (which is exactly the same as for the Earth-Sun system) to generate the Lagrangian for the total system, thus:-
. We can now add this expression to that for the Kinetic Energy of the system (which is exactly the same as for the Earth-Sun system) to generate the Lagrangian for the total system, thus:-
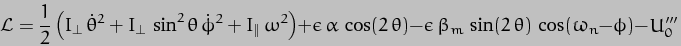
The next step is to apply the Principle of Least Action, which (as you will of course remember!) is

Because the system now has a dependence on 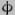 as well as on
as well as on we can differentiate with respect to both variables: the differential of the constant factor
we can differentiate with respect to both variables: the differential of the constant factor 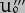 will again be zero in each case.
will again be zero in each case.
With respect to , the result is (unsurprisingly) rather similar to that
in the Earth-Sun case:-
, the result is (unsurprisingly) rather similar to that
in the Earth-Sun case:-

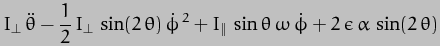

There are two obvious differences however. Because of the asymmetry of the Moon's attraction we cannot assume that precession will be at constant obliquity, and therefore that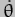 will be zero. The first term in the expression thus cannot be assumed to vanish. The inclination of the Moon's orbit also produces an additional term (the one on the second line) as a consequence of the equivalent term in the Lagrangian.
will be zero. The first term in the expression thus cannot be assumed to vanish. The inclination of the Moon's orbit also produces an additional term (the one on the second line) as a consequence of the equivalent term in the Lagrangian.
Differentiation with respect to 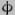 gives us a bit of a problem as it is not clear what the variation in
gives us a bit of a problem as it is not clear what the variation in 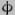 and
and with respect to time might be - that is, after all, what we are trying to find! This part of the differentiation must therefore be left unresolved for the moment, to give:-
with respect to time might be - that is, after all, what we are trying to find! This part of the differentiation must therefore be left unresolved for the moment, to give:-

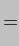
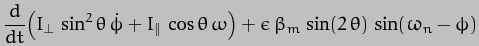
We may not know the exact form that the time dependence of 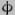 and
and takes but "the real world" tells us that
takes but "the real world" tells us that varies around a mean value of 23.44deg. If we call this value
varies around a mean value of 23.44deg. If we call this value 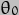 , we can write
, we can write
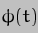
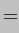
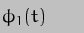
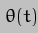
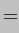
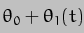
If we now consider the position at time t = 0, when we shall also assume 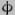 and
and 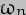 are zero, we can perform the differentiation and substitute the above expressions for
are zero, we can perform the differentiation and substitute the above expressions for 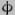 (t) and
(t) and  (t) to give
(t) to give

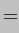
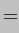

where
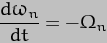 (in radians, because of the approximation we made in calculating cos
(in radians, because of the approximation we made in calculating cos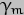 )
)
As in the Earth-Sun case, a number of these terms can be ignored because they are much smaller than the others. We shall see that both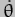 and
and  are small and vary slowly compared to
are small and vary slowly compared to  . This means that both "double dotted" terms (which involve a rate of change of velocity) can be ignored. The term in
. This means that both "double dotted" terms (which involve a rate of change of velocity) can be ignored. The term in  12 can also be ignored because (as mentioned above in the Earth-Sun case) it will be much smaller than the one in
12 can also be ignored because (as mentioned above in the Earth-Sun case) it will be much smaller than the one in 
 1. Eliminating these terms and re-arranging the expressions, we get
1. Eliminating these terms and re-arranging the expressions, we get
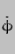
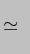
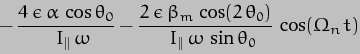
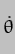
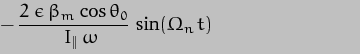
These expressions can be integrated [the reverse process to differentiation] and combined with the expressions in 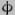 (t) and
(t) and  (t) above. With
(t) above. With  and
and 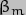 substituted back into the resultant expressions, we get:-
substituted back into the resultant expressions, we get:-
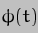
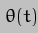
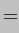

where
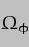
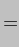
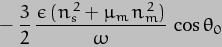
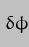
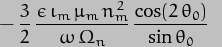
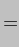
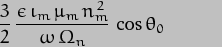
And these are the very final expressions we have been looking for - cue fanfare of trumpets! It is instructive to compare the value we have derived here for 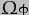 with the one we derived for the Sun alone:-
with the one we derived for the Sun alone:-

The difference clearly lies solely in the 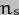 2 factor. If we give this part of the factor the weighting of 1, the contribution added by the
2 factor. If we give this part of the factor the weighting of 1, the contribution added by the 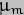
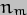 2 part in the Earth-Sun-Moon case is 0.0123 * (365.25636/27.32166)2 = 2.198 [where 27.32166 days is the sidereal orbital period of the Moon]. The overall precession rate due to both Sun and Moon should thus be 3.198 * 15.95 arc-seconds per year, which is 51.01, to give a precession period of 25,405yrs. The currently-adopted rate (as of epoch J2000) is 50.29arc-sec/yr, corresponding to a period of 25,772yrs, so we're pretty close. The discrepancy is mainly accounted for by the fact that the shape of the Moon's orbit is considerably perturbed by the Sun and so the orbital equations (that only apply exactly to perfect ellipses) will not be quite accurate.
2 part in the Earth-Sun-Moon case is 0.0123 * (365.25636/27.32166)2 = 2.198 [where 27.32166 days is the sidereal orbital period of the Moon]. The overall precession rate due to both Sun and Moon should thus be 3.198 * 15.95 arc-seconds per year, which is 51.01, to give a precession period of 25,405yrs. The currently-adopted rate (as of epoch J2000) is 50.29arc-sec/yr, corresponding to a period of 25,772yrs, so we're pretty close. The discrepancy is mainly accounted for by the fact that the shape of the Moon's orbit is considerably perturbed by the Sun and so the orbital equations (that only apply exactly to perfect ellipses) will not be quite accurate.
That deals with the basic precession rate, but what do 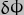 and
and  represent? The first is a variation in the precession rate, the second is a variation in the obliquity of the Earth's spin axis. Taken together, they constitute a phenomenon known as "nutation", so called because
represent? The first is a variation in the precession rate, the second is a variation in the obliquity of the Earth's spin axis. Taken together, they constitute a phenomenon known as "nutation", so called because  imparts a "nodding" motion to the axis, and the Latin for "to nod" is "nutare". Given the title of this additional article, you just knew we'd get to it eventually, didn't you?
imparts a "nodding" motion to the axis, and the Latin for "to nod" is "nutare". Given the title of this additional article, you just knew we'd get to it eventually, didn't you?
To determine their values we have to put numbers to 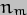 ,
,  and
and 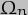 . The first is the angular velocity of the Moon, which is 360 x 365.25636 / 27.32166 degrees per year. The second is the spin rotational velocity of the Earth, which is 360 x 366.25636 degrees per year. The last is the precession rate of the Moon's orbit, which (as noted above) has to be in radians and so is 2 x pi /18.6 radians per year. We also must not forget that
. The first is the angular velocity of the Moon, which is 360 x 365.25636 / 27.32166 degrees per year. The second is the spin rotational velocity of the Earth, which is 360 x 366.25636 degrees per year. The last is the precession rate of the Moon's orbit, which (as noted above) has to be in radians and so is 2 x pi /18.6 radians per year. We also must not forget that 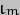 is in radians as well, so has a value of 5.16 x pi/180. Many of the common factors thus cancel out, to give us a final result of 9.60 arc-seconds per year for
is in radians as well, so has a value of 5.16 x pi/180. Many of the common factors thus cancel out, to give us a final result of 9.60 arc-seconds per year for  and -17.97arc-sec/yr for
and -17.97arc-sec/yr for 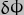 . (If the value of
. (If the value of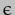 back-calculated from the observed value of
back-calculated from the observed value of 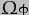 is used, we get 9.36 and -17.52). These values compare well with the currently accepted values of 9.21 and -17.21 respectively.
is used, we get 9.36 and -17.52). These values compare well with the currently accepted values of 9.21 and -17.21 respectively.
In numerical terms therefore, the expressions for the 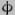 and
and components of the motion of the Earth's spin axis are:-
components of the motion of the Earth's spin axis are:-
where 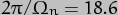 years, i.e. the nutation elements have a periodicity of 18.6 years: the orbital precession rate of the Moon. [Note that, strictly speaking, the period is minus 18.6yrs because the precession is in the opposite direction to the orbital rotation.]
years, i.e. the nutation elements have a periodicity of 18.6 years: the orbital precession rate of the Moon. [Note that, strictly speaking, the period is minus 18.6yrs because the precession is in the opposite direction to the orbital rotation.]
The effect of the simplifying assumptions
During the above analyses I made two types of simplifying assumption - that terms presumed to be small could be ignored and that expressions could be averaged over a complete orbit of the perturbing body. I shall now examine these assumptions in more detail.
Firstly the "small term" simplification, where I said that the rate of change of both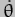 and
and  was small and that
was small and that  was small in comparison to
was small in comparison to  . We can now see that
. We can now see that  changes the most with time, by +/-17.21 over an 18.6yr cycle. A sine (or cosine) wave goes from its maximum value to its minimum value over half a cycle, so the rate of change of
changes the most with time, by +/-17.21 over an 18.6yr cycle. A sine (or cosine) wave goes from its maximum value to its minimum value over half a cycle, so the rate of change of  is 34.42/9.3 = 3.7 arc-seconds per year per year. This is a small number, as stated (and that for
is 34.42/9.3 = 3.7 arc-seconds per year per year. This is a small number, as stated (and that for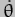 will be even smaller), and so it is indeed safe to ignore both "double dotted" terms. We also know that while
will be even smaller), and so it is indeed safe to ignore both "double dotted" terms. We also know that while  has a mean value of 50.29arc-sec/yr,
has a mean value of 50.29arc-sec/yr,  has a value of 360 x 366.25636 x 3600 arc-sec/yr - a factor of 107 greater. It is thus true that
has a value of 360 x 366.25636 x 3600 arc-sec/yr - a factor of 107 greater. It is thus true that  is very much less than
is very much less than  and so it is also safe to ignore the term in
and so it is also safe to ignore the term in  2.
2.
And now the "averaging" assumption. This is not so much an assumption but a statement of fact - because the variations we are considering are periodic (i.e. they are composed from sine and cosine functions) one can indeed legitimately average over whole orbits. However! One cannot assume that this averaging will not affect the final result. It will not affect its mean value, to be sure, but it will affect its variation with time. In fact, analysis of actually observed values shows that the averages I took have removed small periodic variations in both 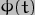 and
and 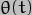 . Both averages were over sin2 expressions, for
. Both averages were over sin2 expressions, for 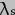 and
and 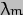 . Because sin2A can be expressed in terms of cos2A, its period is half that of the simple sinA. We might thus expect to find components with a period of half a year and half a lunar month, and indeed we do. The former is quite significant, in fact, with a value of -1.317 in
. Because sin2A can be expressed in terms of cos2A, its period is half that of the simple sinA. We might thus expect to find components with a period of half a year and half a lunar month, and indeed we do. The former is quite significant, in fact, with a value of -1.317 in 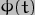 and +0.573 in
and +0.573 in 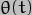 . The latter is much smaller, at -0.228 in
. The latter is much smaller, at -0.228 in 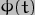 and +0.098 in
and +0.098 in 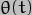 . There is even a component at half the Moon's orbital precession rate which, at +0.207 in
. There is even a component at half the Moon's orbital precession rate which, at +0.207 in 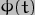 and -0.090 in
and -0.090 in 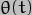 is almost the same magnitude as the half-lunar-month component but of the opposite sign. While not the result of an averaging process, this component arises because of the symmetry of the orientation of the lunar orbit with respect to the general plane of the Solar System. After half a precession period the geometry is the same as at the start, just rotated round the [global] z-axis by 180deg. The basic geometry is also unchanged after half an [apparent] solar orbit or [actual] lunar orbit of course, which is the reason for the half-year and half-lunar-month components. There are then components (mainly in
is almost the same magnitude as the half-lunar-month component but of the opposite sign. While not the result of an averaging process, this component arises because of the symmetry of the orientation of the lunar orbit with respect to the general plane of the Solar System. After half a precession period the geometry is the same as at the start, just rotated round the [global] z-axis by 180deg. The basic geometry is also unchanged after half an [apparent] solar orbit or [actual] lunar orbit of course, which is the reason for the half-year and half-lunar-month components. There are then components (mainly in 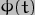 ) caused by the eccentricity of the orbits of Earth and Moon, and also many (many!) other components due to interactions between the basic periodicities, but none is greater than the main four.
) caused by the eccentricity of the orbits of Earth and Moon, and also many (many!) other components due to interactions between the basic periodicities, but none is greater than the main four.
[The numerical values given above were taken from the IAU2000A table of lunisolar nutation components maintained by the collaboration between The Bureau International des Poids et Mesures (BIPM) and the US Naval Observatory (USNO) known as the Conventions Center of the International Earth Rotation and Reference Frames Service (IERS), at web address http://tai.bipm.org/iers/conv2003/conv2003_c5.html ]
Visualisation
While strings of numbers are all very well, it's usually easier to get an idea of what's really going on from a picture or diagram. I've thus prepared a number of illustrations which show the effect that nutation has on and
and 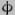 . These take the periodic parts of
. These take the periodic parts of 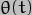 and
and 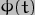 (i.e. ignoring the 23.44deg mean obliquity and -50.29arc-sec/yr mean precession rate) and plot them as sets of graphs in different ways. Successive diagrams in each set include more and more periodic components: click/tap to move through each set. The first diagram in each set has just the basic components calculated above; the next adds the half-yearly component; the next the half-lunar-month component. There is then an expanded version of one of the half-yearly variations, to enable more detail to be seen. The next diagram return us to the situation before the expansion, and then we move on to the half-precession period component; the component due to the eccentricity of the Earth's orbit, and finally that due to the eccentricity of the Moon's orbit. Each graph includes sufficient data points to accurately map an entire 18.6yr cycle (or 1yr in the case of the expanded sections).
(i.e. ignoring the 23.44deg mean obliquity and -50.29arc-sec/yr mean precession rate) and plot them as sets of graphs in different ways. Successive diagrams in each set include more and more periodic components: click/tap to move through each set. The first diagram in each set has just the basic components calculated above; the next adds the half-yearly component; the next the half-lunar-month component. There is then an expanded version of one of the half-yearly variations, to enable more detail to be seen. The next diagram return us to the situation before the expansion, and then we move on to the half-precession period component; the component due to the eccentricity of the Earth's orbit, and finally that due to the eccentricity of the Moon's orbit. Each graph includes sufficient data points to accurately map an entire 18.6yr cycle (or 1yr in the case of the expanded sections).
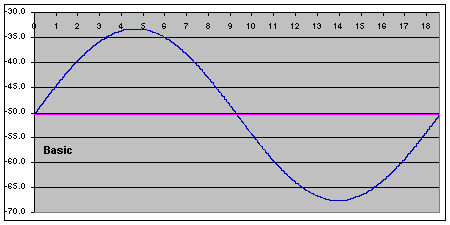 The first set of diagrams has time in years as its x-axis and
The first set of diagrams has time in years as its x-axis and  (i.e. the precession rate) as its y-axis. The pink line indicates the mean value of
(i.e. the precession rate) as its y-axis. The pink line indicates the mean value of  .
.
The basic shape is a sine wave, reflecting this dependency in 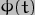 , and shows that nutation causes the precession rate to vary by +/-17.2arc-sec - fully 34.2% of its mean value! It is clear that despite being called "nutation", the phenomenon is much more a change in the precession rate rather than in the obliquity.
, and shows that nutation causes the precession rate to vary by +/-17.2arc-sec - fully 34.2% of its mean value! It is clear that despite being called "nutation", the phenomenon is much more a change in the precession rate rather than in the obliquity.
The second diagram of the set is the most radically different, in that smaller-scale half-yearly fluctuations now appear. There are "37 and a bit" of them, corresponding to the number of half-years in 18.6 full years. The same effect is seen with the next one in the set, and particularly its expanded version which comes after it: 131/2 even smaller-scale fluctuations in a half-year caused by the half-lunar-month component, as one would expect.
The effect of the half-precession-period component is quite noticeable, as it changes the overall shape of the graph, but the final two diagrams exhibit only a slight change due to the small magnitude of the components caused by changes in the orbital eccentricities of Earth and Moon.
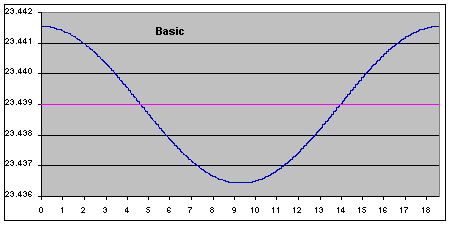 The second set of diagrams again has time in years as its x-axis but now has
The second set of diagrams again has time in years as its x-axis but now has as its y-axis. Note the y-axis scale, by the way - it spans just 0.006 of a degree! The pink line indicates the mean value of
as its y-axis. Note the y-axis scale, by the way - it spans just 0.006 of a degree! The pink line indicates the mean value of .
.
The basic shape is now a cosine wave, reflecting this dependency in  , and shows that nutation causes the Earth's axis to nod to and fro by just 0.0026 of a degree - a mere 0.011% of its mean value!
, and shows that nutation causes the Earth's axis to nod to and fro by just 0.0026 of a degree - a mere 0.011% of its mean value!
The second diagram of this set is again the most radically different in that the smaller-scale half-yearly fluctuations appear. All further diagrams of this set are very similar to those for  , exhibiting the same types of small-scale variations. The addition of the half-precession-period component again changes the overall shape of the graph but the difference in the final two diagrams is almost imperceptible due to the very small effect the eccentricities have on
, exhibiting the same types of small-scale variations. The addition of the half-precession-period component again changes the overall shape of the graph but the difference in the final two diagrams is almost imperceptible due to the very small effect the eccentricities have on  .
.
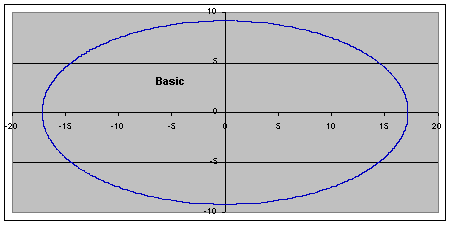 The final set of diagrams has
The final set of diagrams has 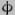 as its x-axis and
as its x-axis and as its y-axis. There is thus no time axis as such: one full circuit of the graph represents the 18.6yr nutation periodicity however.
as its y-axis. There is thus no time axis as such: one full circuit of the graph represents the 18.6yr nutation periodicity however.
Because the major nutation components are 90deg out of phase (as one depends on sine and the other on cosine), and both their periodicities are the 18.6yr span of the graph, the basic shape is just a simple ellipse.
Once again, the half-yearly component makes the greatest difference, turning the simple ellipse into a looped structure. This is due to the much more rapid periodicity of the half-yearly component (182.62 days rather than 6798.38) and its significant magnitude. One might have thought there should be 18.6 x 2 loops, but in fact there is one more than this due to the effect of travelling round the ellipse itself.
The half-lunar-month component results in an interesting "loops within loops" effect: the expanded version allows one to see there are about 121/2 small loops within the big loop. One might have expected there to be 131/2 (the number of lunar months in a year) but, as with the large loops in the ellipse, travelling round the loop changes the number: it is one less this time as the rotations are in the same direction. For the large loops in the ellipse the rotations were in opposite directions, hence the +1. Click again to restore the previous view.
Subsequent diagrams then add in the further components as listed above. Once more, the most interesting one is the half-precession-period component, which imparts a slightly different shape to the whole pattern, but the effect of the Earth's orbital eccentricity is also quite noticeable.
 By "co-ordinate system" I mean the way in which the position of a point in space is specified. The two most common systems are Cartesian, where the position is given relative to a 3-dimensional grid, and Polar, where the position is given in terms of angles and the distance from the origin of the co-ordinates. The diagram shows the same point, P, described by both systems: the Cartesian co-ordinates are x, y, z and the Polar co-ordinates are phi [yellow angle], theta [blue angle], r [radial distance]. However, while this is fine for describing points, when one is working with planes an expression giving (for example) the distance between a point on one plane and a point on another plane involves conversions between the co-ordinate systems describing each plane, which is where all the sines and cosines come in. Lagrange discovered a formalism which, once the initial work to derive its components had been done, did not involve any further conversion gymnastics. He found that if one could derive expressions for the kinetic energy, K, and potential energy, U, of a system, the overall expression representing K - U (called the "Lagrangian" of the system, in his honour) could be manipulated according to simple rules to derive results corresponding to Newtonian mechanics (such things as Force = Mass x Acceleration and Conservation of Momentum). These rules were themselves derived by using the Principle of Least Action, which says that a system proceeds from one state to another via "the line of least resistance" (but expressed mathematically!). The optimal path will usually be a function both of the route taken and the speed at which various parts of the route are traversed. There is a clear analogy here with the different options offered by satnav devices: you can get from A to B either by going slowly on a short country road or faster on a longer motorway. This tradeoff between distance (i.e. change of co-ordinates) and speed (i.e. rate of change of co-ordinates) reflects directly into the precession case - an attempt to change an angular co-ordinate (by the gravitational attraction tending to alter the obliquity) actually results in a change in rotational speed (the motion of precession). The Lagrangian has given us our first insight!
By "co-ordinate system" I mean the way in which the position of a point in space is specified. The two most common systems are Cartesian, where the position is given relative to a 3-dimensional grid, and Polar, where the position is given in terms of angles and the distance from the origin of the co-ordinates. The diagram shows the same point, P, described by both systems: the Cartesian co-ordinates are x, y, z and the Polar co-ordinates are phi [yellow angle], theta [blue angle], r [radial distance]. However, while this is fine for describing points, when one is working with planes an expression giving (for example) the distance between a point on one plane and a point on another plane involves conversions between the co-ordinate systems describing each plane, which is where all the sines and cosines come in. Lagrange discovered a formalism which, once the initial work to derive its components had been done, did not involve any further conversion gymnastics. He found that if one could derive expressions for the kinetic energy, K, and potential energy, U, of a system, the overall expression representing K - U (called the "Lagrangian" of the system, in his honour) could be manipulated according to simple rules to derive results corresponding to Newtonian mechanics (such things as Force = Mass x Acceleration and Conservation of Momentum). These rules were themselves derived by using the Principle of Least Action, which says that a system proceeds from one state to another via "the line of least resistance" (but expressed mathematically!). The optimal path will usually be a function both of the route taken and the speed at which various parts of the route are traversed. There is a clear analogy here with the different options offered by satnav devices: you can get from A to B either by going slowly on a short country road or faster on a longer motorway. This tradeoff between distance (i.e. change of co-ordinates) and speed (i.e. rate of change of co-ordinates) reflects directly into the precession case - an attempt to change an angular co-ordinate (by the gravitational attraction tending to alter the obliquity) actually results in a change in rotational speed (the motion of precession). The Lagrangian has given us our first insight!
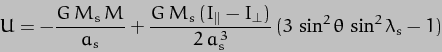


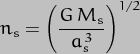 (by Kepler's Third Law)
(by Kepler's Third Law)
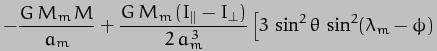

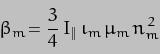
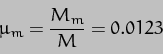
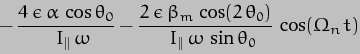
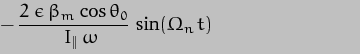
 The first set of diagrams has time in years as its x-axis and
The first set of diagrams has time in years as its x-axis and  The second set of diagrams again has time in years as its x-axis but now has
The second set of diagrams again has time in years as its x-axis but now has The final set of diagrams has
The final set of diagrams has