In this section I shall consider how orbits change as a result of external forces, and in particular I shall explain why a change of orbit speed in one part of an orbit affects the size of another part. I shall also explore more deeply the effect of different types of perturbation (i.e. small but regular disturbances) on the parameters of an orbit. Finally, I shall (in a new section) consider the problem of de-orbiting an object.
The first observation to make is that the orbit speed of the orbiting body is directly related to the "size" of the orbit [more exactly, the distance across the orbit from perihelion to aphelion, called the major axis]. Bodies in smaller orbits go round more quickly. This would seem to imply that if the orbiting body speeds up then it will go into a smaller orbit, but this is clearly not the case - I'm sure everyone is aware that the Space Shuttle (for example) must reduce its speed in order to return to Earth. The resolution of this paradox lies in the fact that an orbiting body can't suddenly jump from one size of orbit to another but must transfer smoothly between them. This requirement implies that the old and new orbits must have [at least] one point in common, where the transition can begin, which tells us that at least one of the orbits must be an ellipse (as it is clearly impossible for two different circular orbits to have a point in common).
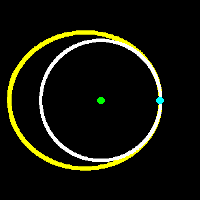
 | I shall first consider the case where the old orbit [in white] is circular and the new one [in yellow] is a larger ellipse. The point in common is thus the perihelion of the ellipse [the blue spot], so the perihelion distance of the new orbit will be equal to the radius of the old, circular, orbit. The major axis of the elliptical orbit is clearly greater than that of the circular one so its orbit speed will be lower but, and this is the crucial bit, it is the average speed that will be lower, not the speed at every point. It is one of the basic properties of an elliptical orbit that orbit speed at perihelion is greater than the average and in fact the maths tells us that the speed at perihelion will always be greater than that of a circular orbit with radius equal to the perihelion distance [if you want to know the details, try looking up "Vis-viva equation" in Google]. In other words, to transfer from our original circular orbit to the perihelion of the larger elliptical orbit we must speed up, despite the fact that the average orbit speed in the new orbit is lower than that in the old one. |
| In the case of an elliptical orbit [yellow] changing into a larger circular orbit [white] the point in common is now the aphelion of the ellipse [the red spot], which will be equal to the radius of the new orbit. The Vis-viva equation tells us that the speed at aphelion will always be less than that of a circular orbit with radius equal to the aphelion distance so once again we must speed up at aphelion to convert our ellipse into a circle despite the fact that, once more, the average speed in the new orbit is lower. This means that to go from a low circular orbit to a high one you have to speed up not once but twice - once to move onto the transfer orbit and once to move onto the new orbit. This manoeuvre actually has a name - the Hohmann orbit, from the name of the chap who first thought of it in connection with spaceflight. | 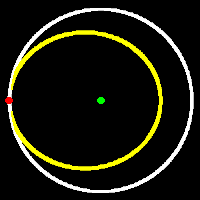 |
 | Taking the case of a transfer from a lower to higher orbit both of which are circular, the Hohmann orbit will thus be an ellipse whose perihelion [the blue dot on the diagram at left] is the radius of the lower orbit and whose aphelion [the red dot] is the radius of the higher orbit. As stated above, the perihelion speed of the transfer orbit is higher than the orbit speed of the smaller circular orbit but the aphelion speed is lower than the orbit speed of the larger circular orbit. This means that orbit speed must be added both to move onto the transfer orbit and also to move off it again. Moving onto the transfer orbit converts an orbit whose perihelion and aphelion are the same (as it is circular) to one whose perihelion is unchanged but whose aphelion is increased. Moving off the transfer orbit leaves the (new) aphelion unchanged but raises the perihelion (as the new orbit is circular again). The overall conclusion is thus that speed added at perihelion will increase the aphelion distance (leaving perihelion unchanged) and that speed added at aphelion will increase the perihelion distance (leaving aphelion unchanged). This result holds generally, not just for the case of circular orbits described here, and of course the converse is also true - a reduction in speed leads to a reduction in distance of the opposite point. |
Another way of looking at it is to consider that an increase in speed gives the orbiting body a bit more energy so it can escape a little farther from its parent body before it is pulled back by gravity, leading to an increase in that part of the orbit opposite from the point of application of the force.
These arguments can of course be set out in reverse if one is moving from a higher orbit to a lower one. In this case is it necessary to reduce speed, both at aphelion in order to enter the transfer orbit and again at the new perihelion to leave it, despite the fact that the average orbit speed in a lower orbit is greater than in a higher one. The classic case where this comes into operation is when a spacecraft fires its engines to return to Earth from, for example, the ISS. To lower its orbit it must reduce its speed and so the engines must be fired in the opposite direction to its direction of travel around the orbit i.e. in a retrograde manner. This is why retro-rockets have the name they do!
Something which is not apparent from all of the above is that the addition or reduction of a given amount of speed has more effect at perihelion, when the orbiting body is moving quickly, than at aphelion when it is moving slowly. This is because the relationship between distance and speed involves the square of the speed - adding or subtracting a small number to or from a small number gives a smaller increase or decrease when squared compared to adding or subtracting the small number to or from a larger one. Thus, 2+1 squared is 9, which is 5 greater than 2 squared, but 3+1 squared is 16, which is 7 greater than 3 squared. Similarly, 2-1 squared is 1, which is 3 smaller than 2 squared, but 3-1 squared is 4, which is 5 smaller than 3 squared. This means it is much easier to change the aphelion distance than the perihelion distance.
Unfortunately, the above explanation based solely on changing orbit speed is slightly too simplistic as it is actually quite difficult to change just the orbit speed. This is because, in general, an orbiting body has two components to its speed - "along the orbit" and "along the radius". The "shape" of an orbit (i.e. its eccentricity and its orientation in space) is determined by the balance between these two components. It might seem strange that a radial component is present but remember that for a body in an elliptical orbit its orbit radius is continually changing - from aphelion to perihelion and back again. Speed is simply the rate of change of a distance so if a distance is changing there must be a speed involved. A circular orbit is a special case of course because, as the orbit radius does not change (by definition!), there is no radial speed component. There are just two other situations when this is true - at aphelion and perihelion in an elliptic orbit. Around aphelion the orbit radius stops increasing and starts to decrease and so exactly at aphelion there is an instant when the rate of change of the radius (and thus the radial speed) is zero - the same argument holds for perihelion. This is crucially important when considering orbit changes!
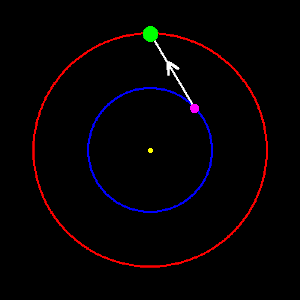 It was the case of the perturbations in the orbit of Ceres by Jupiter that got me interested in this topic, rather than the simpler case of a spacecraft in orbit, and this introduces further complications. As Ceres approaches Jupiter its orbit speed will certainly be increased but this is very unlikely to be just in the "along the orbit" direction. As shown by the diagram on the left [which shows the orbits to scale], there is almost certain to be a radial component as well, because Ceres will get "pulled towards" Jupiter to some extent (as shown by the white arrow). Indeed, at the moment of conjunction (when Jupiter, Ceres and the Sun are in a straight line), the force will be entirely radial! This means that perturbations will not just change the aphelion and perihelion distances but will affect the shape and orientation of the orbit as well. Interestingly, if the radial component due to the perturbation were to be exactly equal and opposite to the radial component already present due to the current shape of the orbit, the net result would be zero. From the discussion above, we can see that this would turn the point of application of the force into the aphelion or perihelion! Critically though, because Jupiter orbits further out than Ceres, the radial component due to its attraction will always be positive and can thus only cancel out an existing negative. The points on an ellipse from aphelion round to perihelion [in the direction of motion] will have negative radial speeds (as the orbit radius is reducing) and so these are the only points that could be transformed in this way. In practice, because the magnitude of the perturbations is small, cancellation would only be possible for points having a very small radial component i.e. those close to aphelion or perihelion. There is thus a small arc of points just after aphelion and just before perihelion that could be affected. This means that the point of aphelion can be moved slightly in the direction of motion and the point of perihelion can be moved slightly against the direction of motion. However, because the perturbations are somewhat stronger at aphelion than at perihelion (due to the decreased Ceres-Jupiter distance), the arc of points capable of being affected would be slightly greater there and so the net "with the motion" shift will be slightly greater than the net "against the motion" shift, leading to an overall movement in the direction of orbital motion. Clearly, if if one of these points moves in a given direction the other must follow it, so the overall effect is to rotate the aphelion-perihelion line in the direction of motion. The longitude of perihelion will thus not only oscillate to and fro but also gradually drift towards greater values. And indeed this is what I found when considering the orbit of Ceres! Isn't it great when things come together nicely?
It was the case of the perturbations in the orbit of Ceres by Jupiter that got me interested in this topic, rather than the simpler case of a spacecraft in orbit, and this introduces further complications. As Ceres approaches Jupiter its orbit speed will certainly be increased but this is very unlikely to be just in the "along the orbit" direction. As shown by the diagram on the left [which shows the orbits to scale], there is almost certain to be a radial component as well, because Ceres will get "pulled towards" Jupiter to some extent (as shown by the white arrow). Indeed, at the moment of conjunction (when Jupiter, Ceres and the Sun are in a straight line), the force will be entirely radial! This means that perturbations will not just change the aphelion and perihelion distances but will affect the shape and orientation of the orbit as well. Interestingly, if the radial component due to the perturbation were to be exactly equal and opposite to the radial component already present due to the current shape of the orbit, the net result would be zero. From the discussion above, we can see that this would turn the point of application of the force into the aphelion or perihelion! Critically though, because Jupiter orbits further out than Ceres, the radial component due to its attraction will always be positive and can thus only cancel out an existing negative. The points on an ellipse from aphelion round to perihelion [in the direction of motion] will have negative radial speeds (as the orbit radius is reducing) and so these are the only points that could be transformed in this way. In practice, because the magnitude of the perturbations is small, cancellation would only be possible for points having a very small radial component i.e. those close to aphelion or perihelion. There is thus a small arc of points just after aphelion and just before perihelion that could be affected. This means that the point of aphelion can be moved slightly in the direction of motion and the point of perihelion can be moved slightly against the direction of motion. However, because the perturbations are somewhat stronger at aphelion than at perihelion (due to the decreased Ceres-Jupiter distance), the arc of points capable of being affected would be slightly greater there and so the net "with the motion" shift will be slightly greater than the net "against the motion" shift, leading to an overall movement in the direction of orbital motion. Clearly, if if one of these points moves in a given direction the other must follow it, so the overall effect is to rotate the aphelion-perihelion line in the direction of motion. The longitude of perihelion will thus not only oscillate to and fro but also gradually drift towards greater values. And indeed this is what I found when considering the orbit of Ceres! Isn't it great when things come together nicely?
In addition to this effect, a radial force will also change the orbit shape, but not simply by changing the orbit speed. Consider that at aphelion the orbit speed is a minimum and the radial speed is zero. The addition of some "outwards" radial speed will mean that the point in question can no longer be the aphelion - it must in fact lie just before the point that will become the new aphelion (remember that the radial speed in an elliptical orbit is positive only from perihelion round to aphelion). The orbiting body still has the same "along the orbit" speed, however, and as the orbit speed at the new aphelion must, by definition, be slower than this it must slow down as it approaches the new aphelion. It must also lose its radial speed, as this is zero at aphelion. The only way these two requirements can be met is for the aphelion distance to increase a little. This will reduce the "along the orbit" speed because the major axis has increased, and it will convert the radial speed to potential energy as the orbiting body is now further from the Sun [This is the same process that happens when a ball thrown upwards slows down and, for an instant, stops moving. Its upwards speed has been converted into potential energy, represented by its greater height above the Earth's surface]. However, the potential energy will re-appear as orbital speed as the orbiting body moves back towards perihelion [in the same way that the ball will convert its potential energy into speed as it falls back down to Earth] resulting in a slightly greater perihelion speed. This will require the perihelion distance to become slightly smaller (as closer-in orbits are faster) and so the end result is consistent - remember that a slower aphelion speed results in a smaller perihelion distance and a faster perihelion speed results in a larger aphelion distance.
If "inwards" radial speed is added at aphelion then the point must lie just after the aphelion of the new orbit. The orbiting body must therefore speed up as it leaves the new aphelion, but the only way it can do this is to fall a little further inwards and thus convert potential energy into orbital speed. This is consistent with the direction it is being pushed by the inwards radial force, so all is well. The end result is, again, a reduced perihelion distance and increased perihelion speed - the latter will of course produce an increased aphelion distance so the overall effect on the orbit shape is (possibly surprisingly) exactly the same as for the outwards radial speed case.

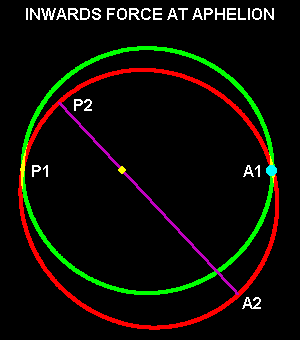
The above diagrams (taken from an orbit simulation program) show the effects - the rotation of the aphelion-perihelion line and the change in distances. Actual perturbations are rather smaller, of course! In each case the original orbit is shown in green and the new orbit in red: orbital motion is assumed to be anti-clockwise. The radial force is applied at the original aphelion - point A1. A2 and P2 are the new aphelion and perihelion respectively.
The situation at perihelion is simply the reverse of that described above. Outwards radial speed applied at perihelion will mean that this point must lie just after the new perihelion. The orbiting body will thus need to slow down as it leaves the new perihelion, which it can do by moving outwards, in the direction of the applied force. This will produce an increased aphelion distance and thus reduced aphelion speed. An inwards radial force will move the former perihelion to a point just before the new perihelion, requiring an increase in speed as the new perihelion is approached which can be gained by an inwards movement, again in the direction of the applied force. As before, this increased speed will in its turn lead to an increase in aphelion distance. The outwards and inwards cases thus again have the same effect on the orbit shape. Indeed, simulations I have done indicate that a given amount of added radial speed will have exactly the same effect on the orbit shape whether applied at aphelion or perihelion and whether directed inwards or outwards - definitely not what one would expect intuitively! It must be noted though that this method of increasing the aphelion distance is much less efficient than adding "along the orbit" speed at perihelion, so is not normally used for this purpose by spacecraft. It is used to change the orientation of the orbit, however, in order to align one orbit with another when performing rendezvous and docking manoeuvres, for example.
So, to summarise :- a radial force at either aphelion or perihelion (whether directed towards the centre or away from it) will increase the aphelion distance and also decrease the perihelion distance, but by a smaller amount. It will also rotate the direction of the aphelion-perihelion line: Against the direction of orbital motion if the force is towards the centre at aphelion or away from the centre at perihelion, and in the direction of motion if the force is away from the centre at aphelion or towards the centre at perihelion.
[Note that, in principle, an orbit can be converted from elliptical to circular if the force were to be applied at exactly the correct place in the orbit such that, after the cancellation of the radial speed, the remaining along-the-orbit speed was just that required by the circular orbit corresponding to the orbital radius at that point. While this is indeed possible for spacecraft, planetary perturbations are much too small to be able to cause this to happen.]
There is a third type of force that could act on an orbiting body - one at right angles to the plane of its orbit i.e. "out of the paper" or "into the paper" relative to an orbit drawn on a page. This does not change the orbit speed (either "along the orbit" or radially), so does not lead to a change in the orbit shape, but will instead change the orbit's inclination i.e. its "tilt". The mechanism for this is exactly what one might expect - pushing down on one edge of the orbit will cause the other to rise, leading to a change in tilt (think of the analogy of the piece of paper again). However, this will produce a secondary effect because you are pushing down on an object which is rotating. Classical mechanics tells us that when a rotating object is forced to increase the tilt of its axis of rotation, the axis will move in the direction of the rotation. For example, if you try to push over a top which is spinning anti-clockwise its axis of rotation will move from right to left as well as away from you. In the case of asteroid perturbations the orbital inclination is always being forced to reduce, as that of Jupiter is very small (about 1.3deg). Given that the asteroid is orbiting anti-clockwise, the effect will thus be to cause the axis of rotation of its orbit (and thus the orbit as a whole) to twist in a clockwise direction. This is the reason that the most-northerly point of the orbit will slowly move round clockwise, as discovered in the same section on Ceres as the effect of perihelion precession noted above.
And now we have established the basic principles, we can apply them to a practical, but rather unusual, example.
This question arose as a result of a discussion on the follow-up programme to the January 2014 edition of the BBC "Stargazing Live" TV programme. A viewer, aware of the infamous "tool bag" incident (where an astronaut working on the ISS lost control of a tool bag, which slowly floated away from her and eventually fell back to Earth), asked how easy it would be to deliberately cause on object to come out of orbit. The answer given was that throwing an object towards the Earth from the ISS would cause it to fall to Earth because "the orbital and towards-Earth velocities are independent". This (rather confused) statement is [largely] incorrect however. Adding radial velocity to an orbiting object (e.g. by throwing it towards the Earth) will indeed alter its orbit but not in the simplistic sense of immediately causing it to re-enter. The comment about the velocities being independent is not true in an orbital situation, and is definitely not true in the sense implied by the programme presenter i.e. the suggestion that the (large) orbital velocity causes the object to go round the Earth while the (small) radial velocity determines how high it does this. In fact, it is the balance between the radial and orbital velocities which determines the shape of the orbit, and this continuously shifts due to the interchange between the kinetic and (gravitational) potential energies of the orbiting object. To re-cap what we saw above, an applied change in radial velocity will simply decrease the perigee and increase the apogee, in much the same way as changes in orbital velocity can (depending on where on the orbit the change is applied). Perhaps surprisingly, this is true wherever round the orbit the additional radial velocity is applied and whether it is directed towards the Earth or away from it! The change in velocity will also cause the apogee/perigee line to move and the orbital eccentricity to change. None of these changes will immediately cause the object to come out of orbit though, as was seemingly implied by the answer given.
Now of course a decrease in perigee could, if great enough, cause the object to re-enter but the effectiveness of a radial velocity change in achieving a given decrease in perigee is very much less than that produced by reducing the orbital velocity at apogee. In other words, if one wished to de-orbit an object the best way to do so would be to wait until apogee is reached and then throw it against the direction in which it is orbiting (thus decreasing its orbital velocity). Even so, whether an astronaut could apply sufficient force to achieve a rapid de-orbit of a significantly massive object is very doubtful. In round numbers, to cancel out just 10% of its orbital speed of about 27,600km/hr (17,250mph) would require the astronaut to accelerate the object at 78G and retain a firm grip on it for 1sec while doing so. Most unlikely to be possible, even on the Earth let alone floating round weightless in a bulky spacesuit. To put it another way, the speed the object would have to be given to lose just this 10% of its orbital velocity (2500ft/sec) compares quite well to that of a 50-calibre sniper bullet (3000ft/sec). So - immediately de-orbit an object by throwing it towards the Earth? I don't think so! The fact that the tool-bag fell back to Earth after a little over 36 weeks having been given just a small nudge is not a contradiction of the above but simply an illustration of the fact that minuscule decelerations can have massive effects if continued for long enough. To have removed the tool-bag's entire orbital velocity would have required a deceleration of a mere 0.00084G over that time, which could easily be provided by the very tenuous atmosphere still present at the ISS's orbital height.
Having shown that achieving an immediate de-orbit by the means which seemed to be implied by the question is impossible, I will now consider the second possibility of doing so: by reducing the perigee sufficiently that the object would fall to Earth without completing a further orbit. Research using an orbit simulation program showed that at the orbital height of the ISS (about 415km) it would require a decrease in orbital speed of about 440km/hr (273mph) to reduce the perigee by the required amount. This is 1.6% of its orbital speed - a considerably easier proposition than the 10% used as in the previous example, but still requiring a acceleration of 12.6G for 1sec. The required reduction in speed should be compared to the speed off the club-face of a golf ball driven by Tiger Woods - 288km/hr (180mph). Clearly, achieving this speed by throwing the object would be totally impossible, and even in the near-vacuum of space it is incredibly unlikely that a drive could reach the required speed, despite the great effort made by cosmonaut Mikhail Tyurin on one occasion (no doubt having to wear a spacesuit didn't exactly help!). Other forms of propulsion (gun-like, for example) could clearly succeed, and of course any [substantial] reduction in speed would cause an eventual de-orbit, particularly taking into account the effect of atmospheric drag as the object got closer to the Earth, but this wasn't what was [seemingly] being asked.
The question thus seems to divide into three sub-topics:-
1) Is it possible to cause an object to immediately de-orbit by throwing it towards the Earth? No - it is not. Not even close! It is also not possible to do so by throwing it against the direction of orbital travel.
2) Is it possible for an "unaided" astronaut to cause an object to de-orbit without completing a further orbit? No - for all practical purposes it is not. To do so would require it to be "thrown" about 50% faster than even a golf ball can be driven on Earth.
3) Is it possible for an unaided astronaut to cause an object to de-orbit "reasonably quickly"? Yes, I think it is in principle but maybe not in practice. For example, if a small object could be subjected to a "plausible" golf drive, as described above, its perigee would drop to just 135km (84mls). Atmospheric effects become noticeable for re-entering spacecraft at about 120km, and so at 135km the appreciable atmospheric drag would lead to a rapid de-orbit. More realistically, for a throw of 128kph (80mph) - easily obtainable with a cricket ball, at least on Earth - the perigee would drop to 285km (177mls) which, while not causing a rapid de-orbit, would probably get there in a few weeks. However, it is extremely doubtful whether such a drive would be practical in space, and even a throw of this magnitude is going to be hard to achieve.